【データ構造について】絞り込み機能の実装で発生した課題と解決策

絞り込み機能の実装の中で、ReactのStateとして管理しているカテゴリの制御にて発生した課題と、それをどのように解決したのかという事についての記事です。

絞り込み機能の要件と前提

今回制作する絞り込みの機能要件

• 絞り込み条件は3階層の構造となっている
• 1階層目の項目はAND検索
• 2,3階層目の項目はOR検索
• 1階層目には3つの項目が存在する
• 3階層目まである項目は1階層目の1つ目の項目
• 絞り込みに使用する要素は記事のカテゴリIDで、記事本体についているカテゴリIDを元に絞り込む。
• カテゴリIDに重複はない。
• urlのパラメータにカテゴリIDをつけ、その情報を元に絞り込み検索を行いたい。
• urlを元に絞り込む場合、選択した内容も反映される事（3階層目の項目もアクティブになり、その親の2階層目もアクティブになる）

制作における前提

• 絞り込み項目の内容は後から変更になるかもしれない。
• 最大3階層、AND検索、OR検索は変わらないが、2階層目までしかなかった項目が3階層になったり、その逆もありえる。
• 1,2,3階層目、それぞれの項目の数も変化するかもしれない。

絞り込み条件を選択するUIのイメージ

各カテゴリ、各記事が持っているデータと構造

カテゴリ、記事のデータはどちらもjson形式で取得した後、object形式で変数に格納されています。

カテゴリ

カテゴリ情報は以下のような構成で保持されています。

「’」シングルクォーテーションで囲われている文字はその文字列がプロパティ名となり、囲われていない文字は各カテゴリの情報が動的にはいります。

例えば『categoryId』はカテゴリのid、すなわち、その重複のない数字（そのカテゴリのID）が入ります。

{
  Type:{
    categoryId:{
      'title': 'string',
      'id': 'number',
      'isActive': 'boolean',
      'child': {
        categoryId: {
          'title': 'string',
          'id': 'number',
          'isActive': 'boolean',
        },
      },
    },
  },
}

今回は、選択したカテゴリのボタンの色を変更する必要がありますが、そのカテゴリが選択された状態なのか、選択されていない状態なのかという情報はこちらのデータで管理します。

isActiveプロパティがそれを担っており、true/falseで管理しています。

記事

記事情報は以下のような構成で保持されています。

「’」シングルクォーテーションで囲われている文字はその文字列がプロパティ名となり、囲われていない文字は各カテゴリの情報が動的にはいります。

例えば『articleId』は記事のid、すなわち、その重複のない数字（その記事のID）が入ります。

{
  articleId:{
    'id': 'number',
    'title': 'string',
    'link': 'string',
    'descForArchive': 'string',
    'categorys': {
      categoryId: {
        'title': 'string',
      },
    },
  },
}

情報やデータはグラフで考える

この状態でいきなりプログラムを考えてもよいのですが、情報を整理するためにカテゴリデータをグラフに置き換えて考えましょう。

グラフに置き換えて考える事で余計な情報を排除することができ、理解しやすくなります。

また、抽象的になるので他の問題にも転用しやすくなる事もメリットです。

情報をグラフに置き換えるとは

情報をグラフに置き換えるとは情報どおしの関係を辺と点で結んで表す事を言います。

数学のx座標y座標のことではありません。

グラフ理論[wiki]です。

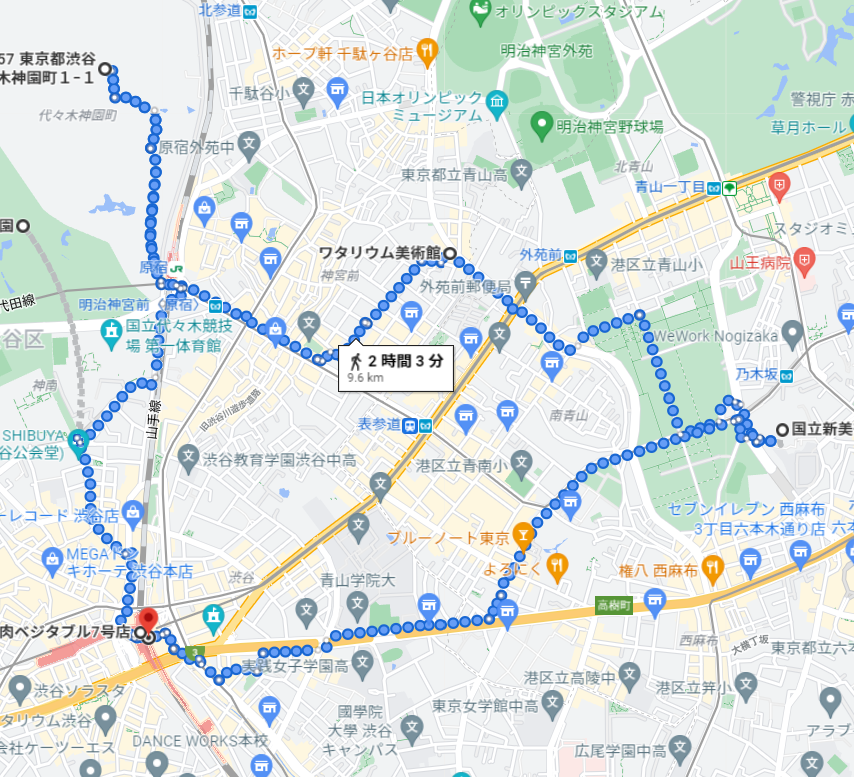
例えば以下のように、全てのスポットを効率よく周りたいので最短の経路を見つけたいといった問題が有名です。

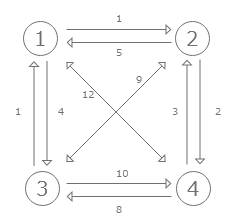
地図で考えると余計な情報が沢山含まれており、複雑になるので、必要な情報のみを抽出し、以下のように辺と点で表してから考えます。

これと同じように、カテゴリデータをobjectのままで考えようとすると理解が難しくなるのでグラフにして考えます。

カテゴリデータのグラフ

カテゴリデータをグラフにしますが、今回必要なものはカテゴリの親子関係になります。そのカテゴリがどういった情報を持っているのかは気にする必要はありません。

ですので、必要なものは以下のになります。

{
  Type:{
    categoryId:{
      'child': {
        categoryId: {
        },
      },
    },
  },
}

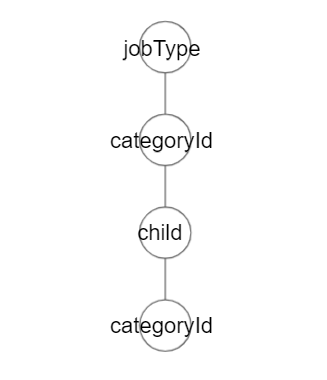
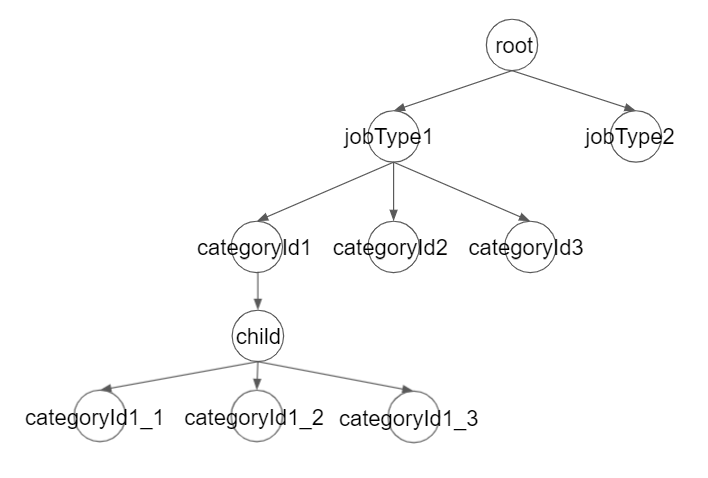
これをグラフにすると以下のようになります。

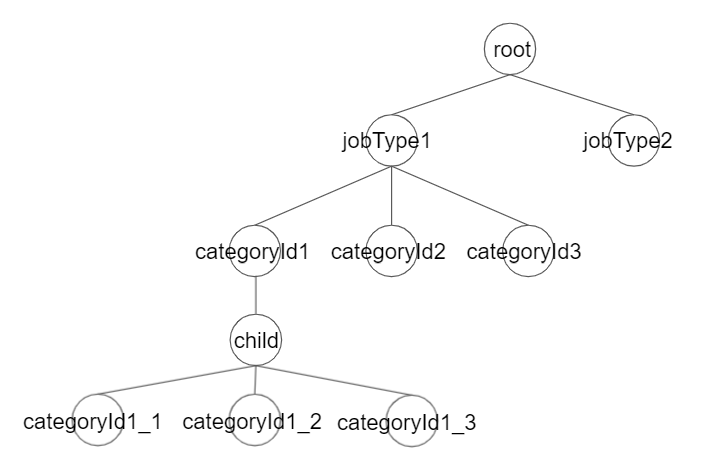
これは型としての構造なので、ここにデータが入ると以下のようなイメージになります。

グラフの点の部分を「ノード」といい、グラフの辺の部分を「エッジ」と呼ぶのでこちらでもそれぞれノード、エッジで話を進めます。

各ノードにはjobTypeやcategoryIdなど、データ型に適した値が入ってきます。

ちなみにこのようなグラフを無向グラフと言います。

今回の場合は情報へのアクセスが必要となってきますので、どこから各ノードにアクセスができるのかという情報も必要になってきます。

グラフに向きを与えましょう。

このようなグラフを有向グラフと言います。

見てわかるようにobjectは親から子を参照する事しかできず、子から親を参照する事ができない構造となっています。

単純な実装方法

まず、初めに単純に選択した条件で記事を絞り込む方法を考えました。

単純な絞り込み方法とは、探したい情報が見つかるまで各ノードをしらみつぶしに巡回する方法です。